Blog do IBRE

Em recente post no blog do IBRE, Samuel Pessôa apontou dois momentos de quebra estrutural na série de taxa de crescimento da economia brasileira entre 1900 e 2019. A primeira quebra teria acontecido por volta de 1916, enquanto a segunda teria ocorrido em 1980. No entanto, não foram apresentados resultados de testes formais de quebra estrutural. Neste post, apresento uma aplicação simples da metodologia de Bai e Perron (2003), utilizando tanto o código original para GAUSS (Perron 2004) quanto o pacote ‘strucchange’ do R (Zeileis et al. 2003). [1]

A série utilizada foi a taxa de crescimento da renda per capita. Como esperado, os testes de raiz unitária indicaram estacionariedade da série. A partir disso, investiguei em primeiro lugar a existência de alguma quebra, partindo da hipótese nula de ausência de quebras. Zeileis et al. (2003) aconselham uma metodologia mais gráfica, utilizando os testes supF e OLS-CUSUM, que apontaram a existência de pelo menos uma quebra em 1980. Bai e Perron (2003) recomendam o uso dos testes UDmax e WDmax, que indicaram a existência de ao menos uma quebra a 10% de significância. Utilizamos os parâmetros recomendados por Bai e Perron (2003): máximo de cinco quebras (m = 5) com 15% de tamanho mínimo para cada segmento (h = 0.15).

Esta dificuldade em identificar a presença ou não de quebras pode ser explicada pela estrutura da série. Bai e Perron (2003, p. 15) relatam que os testes podem indicar ausência de quebras quando, na realidade, “duas quebras estão presentes e o valor do coeficiente retorna para seu valor original depois da segunda quebra”. Esse parece ser o caso desta série de dados (vide Figura 1). Em situações como essa, Bai e Perron (2003) assinalam que uma estratégia sequencial de identificação de quebras pode não funcionar e recomendam o uso do teste supF(l+1|l). Esse teste, no caso, não tem comando automático no pacote ‘strucchange’, o que me levou a utilizar também o código original de Perron para o GAUSS.

Em geral, o conjunto dos testes indica duas quebras estruturais: 1918 e 1980. O teste supF(l+1|l) indica a existência de duas quebras. Já o método BIC, conhecido critério de informação, também recomenda duas quebras. Por fim, o teste LWZ, uma modificação do BIC com parâmetros mais punitivos, não encontra quebras. Os resultados da seleção via critérios de informação são consistentes com a observação de Bai e Perron (2003): o BIC funciona bem quando há quebras, mas funciona mal quando não há quebras; já o critério LWZ tem desempenho melhor sob a hipótese nula de ausência de mudança estrutural, mas é ruim quando existem quebras. Como dito antes, é improvável que não tenha havido ao menos uma quebra em 1980. Assim, a escolha de duas quebras parece ser a mais adequada.

Vale ressaltar que apenas um modelo com cinco quebras indicaria algum ano da década de 1930 como ponto de quebra (no caso, seriam os anos de 1918, 1936, 1956, 1980 e 1999). Nenhum dos testes recomendados, no entanto, apontou para a existência de cinco quebras. Antes de 1936, os anos de 1956 e 1999 seriam inclusive candidatos mais aptos a pontos de mudança estrutural. É claro que isso se trata de uma aplicação simples de um modelo univariado e não deve ser tomado como evidência conclusiva. Contudo, trata-se de informação relevante para o debate sobre o período – e que chama atenção para a importância da industrialização ocorrida antes da década de 1930, como já registrado por reconhecida literatura (ver, por exemplo, Dean 1969, Fishlow 1972, Suzigan 2000, Marson 2015). A datação da quebra em 1918 possivelmente se deve à recuperação das exportações logo após a Primeira Guerra e à expansão industrial na década de 1920.

A Figura 1 mostra a série de taxas de crescimento considerando duas quebras, enquanto a Tabela 1 apresenta os resultados dos testes conforme o código de Perron (2004) no GAUSS.

Figura 1: Modelo de quebras estruturais (duas quebras), série de taxa de crescimento do PIB per capita, Brasil, 1900-2019

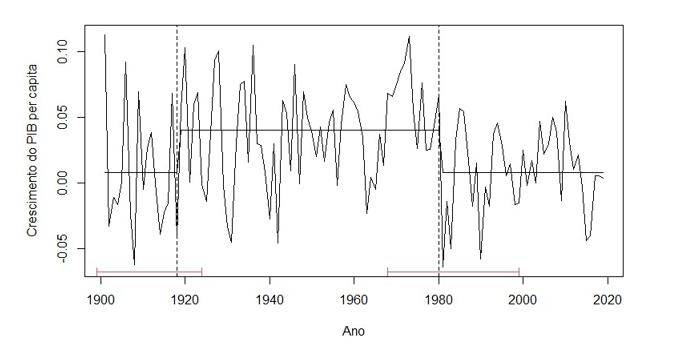
Tabela 1: Testes de quebra estrutural endógena Bai-Perron, taxa de crescimento do PIB per capita, Brasil, 1900-2019

As opiniões expressas neste artigo são de responsabilidade exclusiva do autor, não refletindo necessariamente a opinião institucional da FGV.

Referências

Bai, J and Perron, P. (2003), “Computation and analysis of multiple structural change models,” Journal of Applied Econometrics 18, 1-22.

Dean, W. (1969), The industrialization of São Paulo. Austin and London: University of Texas Press.

Fishlow, A. (1972). Origins and consequences of import substitution in Brazil. In: di Marco, L. E. International economics and development: essays in honor of Raul Prebisch. New York and London: Academic Press, 311-365

Marson, M. (2015), “A industrialização brasileira antes de 1930: uma contribuição sobre a evolução da indústria de máquinas e equipamentos no estado de São Paulo, 1900-1920”. Estudos Econômicos (São Paulo), 45(4), 753-785.

Perron, P. (2004), “Computation and hypothesis testing in models with multiple structural changes”, GAUSS code, revised version.

Suzigan, W. (2000), Indústria brasileira: origem e desenvolvimento, 2 ed. São Paulo: Hucitec e Ed. da Unicamp.

Zeileis, A. et al. (2003), “Testing and dating of structural changes in practice”, Computational Statistics and Data Analysis, 44, 109-123.